6DOF

Linapod 6DOF

Release status: Concept

Description	Cinematica a sei gradi di libertà per Linapod sviluppata dall'ISW.
License	CC-BY-SA
Author	User:Bruno.laterza
Contributors
Based-on	[[]]
Categories	Principles
CAD Models
External Link

sorry

soon I will translate.

---

Espongo le equazioni per la cinematica inversa a sei gradi di libertà di linapod, un robot sviluppato dall'ISW

Si introduce circa il funzionamento della cinematica, e si presuppone che le catene cinematiche siano funzionanti.

Con questi calcoli si vuole realizzare una macchia con sei gradi di libertà, in grado di muovere l'utensile in tutte le posizioni <math>(x,y,z)</math> e in tutte le rotazioni <math> (\alpha, \beta, \gamma)</math>.

Linapod

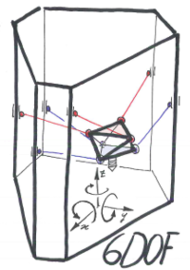
Linapod è un robot a cinematica parallela con sei gradi di libertà. Per poterli gestire si usano sei attuatori lineari prismatici.

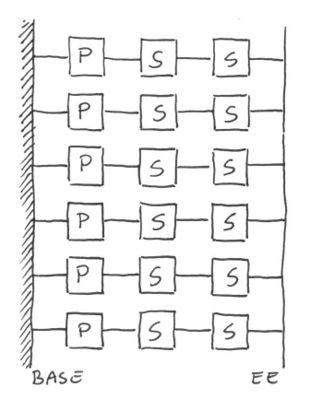
Le sei catene cinematiche sono composte da tre giunti P-S-S (prismatico sferico sferico). il giunto lineare P è motorizzato, e tramite le posizioni dei sei giunti P si determina la posizione nei 6 gradi del'End-Effector.

catena cinematica parallela P-S-S

Quindi si definisce:

Base: sistema di riferimento solidale con l'ambiente detto anche <math>{\left \{ A \right \}}</math>;

End-Effector: sistema di riferimento solidale con l'attuatore della macchina detto anche <math>{\left \{ EE \right \}}</math>.

---

Definizioni

si definiranno due sistemi di riferimento, Base <math>{\left \{ A \right \}}</math> e End-Effector <math>{\left \{ EE \right \}}</math>. Inoltre dove necessario i punti avranno un prefisso che indicherà a che sistema di riferimento al si appoggiano.

Base

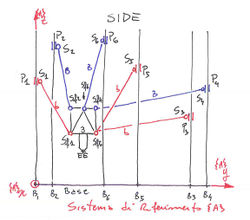
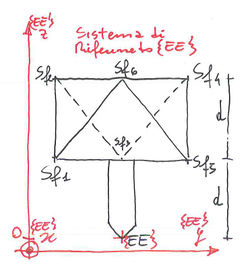
definisco il sistema di riferimeto della base e che indicherò con <math>{\left \{ A \right \}}</math> come da figura.

Base top in <math>{\left \{ A \right \}}</math>

Base side in <math>{\left \{ A \right \}}</math>

Punti <math> ^{\left \{ A \right \}}B_i , i=1..6 </math> solidali al <math>{\left \{ A \right \}}</math> in coordinate omogenee.

<math> ^{\left \{ A \right \}}B_1:\left(\frac{\sqrt{3}d}{2},0,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_2:\left(0,\frac{d}{2},0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_3:\left(0,D + \frac{d}{2},0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_4:\left(\frac{\sqrt{3}d}{2},D + d,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2} + d,0,1 \right)</math>;

<math> ^{\left \{ A \right \}}B_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2},0,1 \right)</math>;

i <math> ^{\left \{ A \right \}}B_i</math> sono i sei assi su cui appoggiano i giunti prismatici.

Punti <math> ^{\left \{ A \right \}}P_i , i=1..6 </math> solidali al <math>{\left \{ A \right \}}</math> in coordinate omogenee rappresentano i sei punti comandati dagli attuatori, e i <math> c_i </math> rappresentano le variabili da comandare con gli attuatori.

<math> ^{\left \{ A \right \}}P_1:\left(\frac{\sqrt{3}d}{2},0,c_1,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_2:\left(0,\frac{d}{2},c_2,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_3:\left(0,D + \frac{d}{2},c_3,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_4:\left(\frac{\sqrt{3}d}{2},D + d,c_4,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_5:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2} + d,c_5,1 \right)</math>;

<math> ^{\left \{ A \right \}}P_6:\left(\frac{\sqrt{3}(D+d)}{2},\frac{D}{2},c_6,1 \right)</math>;

inoltre i sei braccetti che congiungono l'End-Effector sono di due misure <math> B </math> e <math> b </math>.

---

End-Effector

Base top in <math>{\left \{ A \right \}}</math>

Base side in <math>{\left \{ A \right \}}</math>

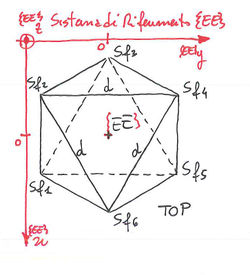
definisco, come in figura, i sei punti <math> Sf_i , i=1..6 </math> dei giunti sferici dell'end effector in coordinate omogenee riferiti al sistema di riferimento <math>{\left \{ EE \right \}}</math>. Il sistema di riferimento <math>{\left \{ EE \right \}}</math> è solidale all'End-Effector e l'origine coincide con la punta dell'attuatore.

<math> ^{\left \{ EE \right \}}Sf_1:\left(\frac{d}{2\sqrt{3}},-\frac{d}{2},d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_2:\left(-\frac{d}{2\sqrt{3}},-\frac{d}{2},2 d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_3:\left(-\frac{d}{\sqrt{3}},0,d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_4:\left(-\frac{d}{2\sqrt{3}},\frac{d}{2},2 d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_5:\left(\frac{d}{2\sqrt{3}},\frac{d}{2},d,1 \right)</math>;

<math> ^{\left \{ EE \right \}}Sf_6:\left(\frac{d}{\sqrt{3}},0,2 d,1 \right)</math>;

Matrice di rototraslazionezione Omogenea

Matrice:

definisco la matrice di rotazione del S.d.r. <math>{\left \{ EE \right \}}</math> (End Effector) rispetto <math>{\left \{ A \right \}}</math> (Base). tutti i conti sono fatti in coordinate omogenee.

nel definirla uso rotazione con angoli RPY rispetto alla terna fissa <math>{\left \{ A \right \}}</math>} definisco le due SOLE rotazioni:

- Prima intorno all'asse 'x' di rotazione <math> \gamma</math>

- Seconda intorno all'asse 'y' di rotazione <math> \beta</math>

inteso verso antiorario positivo.

<math> ^{\left \{ A \right \}}T_{\left \{ EE \right \}} : \begin{bmatrix} \cos\beta & \sin\beta \sin\gamma & \sin\beta \cos\gamma & t_1 \\ 0 & \cos\gamma & -\sin\gamma & t_2 \\ -\sin\beta & \cos\beta \sin\gamma & \cos\beta \cos\gamma & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} </math>

questa matrice applicata ai punti <math>^{\left \{ EE \right \}}Sf_i , i=1..0</math> me li riferisce al sistema di riferimento <math>{\left \{ A \right \}}</math>}. facendo così ho i punti dell'End-Effector roto-traslati riferiti al <math>{\left \{ A \right \}}</math>} e facili da usare per calcolare la cinematica inversa della macchina.

Punti rototraslati

applico la matrice ai punti:

<math> ^{\left \{ A \right \}}Sf_i := ^{\left \{ A \right \}}T_{\left \{ EE \right \}} \cdot ^{\left \{ EE \right \}}Sf_i </math>

<math> ^{\left \{ A \right \}}Sf_i := \begin{bmatrix} \cos\beta & \sin\beta \sin\gamma & \sin\beta \cos\gamma & t_1 \\ 0 & \cos\gamma & -\sin\gamma & t_2 \\ -\sin\beta & \cos\beta \sin\gamma & \cos\beta \cos\gamma & t_3 \\ 0 & 0 & 0 & 1 \end{bmatrix} \cdot ^{\left \{ EE \right \}}Sf_i </math>

quindi i sei punti riferiti ad <math> {\left \{ A \right \}} </math> risultano:

<math> ^{\left \{ A \right \}}Sf_1 = \begin{pmatrix}t_1-\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) -\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3-\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_2 = \begin{pmatrix}t_1-\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) -\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3-\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_3 = \begin{pmatrix}t_1+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{\sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) \cr t_3+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{\sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_4 = \begin{pmatrix}t_1+\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) +\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3+\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_5 = \begin{pmatrix}t_1+\frac{\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr t_2-d\cdot \mathrm{sin}\left( \gamma\right) +\frac{d\cdot \mathrm{cos}\left( \gamma\right) }{2}\cr t_3+\frac{\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{sin}\left( \gamma\right) }{2}+\mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{2\cdot \sqrt{3}}\cr 1\end{pmatrix} </math>;

<math> ^{\left \{ A \right \}}Sf_6 = \begin{pmatrix}t_1+2\cdot \mathrm{sin}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) +\frac{\mathrm{cos}\left( \beta\right) \cdot d}{\sqrt{3}}\cr t_2-2\cdot d\cdot \mathrm{sin}\left( \gamma\right) \cr t_3+2\cdot \mathrm{cos}\left( \beta\right) \cdot d\cdot \mathrm{cos}\left( \gamma\right) -\frac{\mathrm{sin}\left( \beta\right) \cdot d}{\sqrt{3}}\cr 1\end{pmatrix} </math>;

Risoluzione cinematica inversa

Definizione Sfere

adesso che si hanno definito tutti i punti in <math> {\left \{ A \right \}} </math> risolvo vincolando i punti <math> ^{\left \{ A \right \}}Sf_i </math> alle sfere di centro <math> ^{\left \{ A \right \}}P_i </math> e di raggio opportuno: <math> B </math> o <math> b </math>.

quindi:

<math> ^{\left \{ A \right \}}S_i : = {{\left( x - ^{\left \{ A \right \}}P_i(x) \right) }^{2}} + {{\left( y - ^{\left \{ A \right \}}P_i(y) \right) }^{2}} + {{\left( z - ^{\left \{ A \right \}}P_i(z) \right) }^{2}} - b^2 </math>

che facendo le opportune sostituzioni si hanno:

<math> ^{\left \{ A \right \}}S_1 : = {{\left( z-c_1\right) }^{2}}+{{y}^{2}}+{{\left( x-\frac{\sqrt{3}\cdot d}{2}\right) }^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_2 : = -{{B}^{2}}+{{\left( z-c_2\right) }^{2}}+{{\left( y-\frac{d}{2}\right) }^{2}}+{{x}^{2}} </math>

<math> ^{\left \{ A \right \}}S_3 : = {{\left( -D+y-\frac{d}{2}\right) }^{2}}+{{\left( z-c_3\right) }^{2}}+{{x}^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_4 : = {{\left( -D+y-d\right) }^{2}}-{{B}^{2}}+{{\left( z-c_4\right) }^{2}}+{{\left( x-\frac{\sqrt{3}\cdot d}{2}\right) }^{2}} </math>

<math> ^{\left \{ A \right \}}S_5 : = {{\left( x-\frac{\sqrt{3}\cdot \left( D+d\right) }{2}\right) }^{2}}+{{\left( -\frac{D}{2}+y-d\right) }^{2}}+{{\left( z-c_5\right) }^{2}}-{{b}^{2}} </math>

<math> ^{\left \{ A \right \}}S_6 : = {{\left( x-\frac{\sqrt{3}\cdot \left( D+d\right) }{2}\right) }^{2}}+{{\left( y-\frac{D}{2}\right) }^{2}}-{{B}^{2}}+{{\left( z-c_6\right) }^{2}} </math>

Vincolare i punti dell'End-Effector alle sfere

Le sfere definite come sopra sono l'insieme di tutti i punti che possono essere presi dai <math> ^{\left \{ A \right \}}Sf_i </math> per ogni i=1..6. inoltre le sfere sono definite da un unica grandezza che è la <math> c_i </math>, che è solidale all'attuatore scelto.

quindi ai valori <math> (x,y,z) </math>, incognite della sfera, sostituisco i relativi <math> ^{\left \{ A \right \}}Sf_i </math> ottengo una equazione di secondo grado in <math> c_i </math>. una delle due soluzioni dell'equazione è il legame tra <math> c_i </math> i=1..6 e i sei gradi di liberà dell'<math> {\left \{ EE \right \}}</math>.

Soluzioni Cinematica Inversa

le sei equazioni risolutive le trovate in File:LinaPod 6Dof r1.zip il software per gestirlo è Maxima un potente software di CAS (Computer Algebra System).

(sono nella sezione 5 sotto il nome della funzione:'soluzione_2_c_i(D,d,B,b,t_1,t_2,t_3,be,ga)' con i=1..6)

inoltre i conti fatti li ho verificati con un CAD meccanico verificandone la coerenza.

6DOF o 5DOF

la scelta di creare una macchina a sei gradi di libertà (6DOF) è stata fatta pensata per rendere la macchia più semplice e simmetrica possibile.

per il tipo di lavorazione (stampa 3D) sono sufficenti cinque gradi di libertà per fare le lavorazioni.

Prospettive

spero che qualcuno serva questo lavoro per continuare lo studio e la realizzazione di macchine che gestiscano i sei gradi di libertà, in particolare si deve sviluppare il software per generare il percorso utensie (CAM software) [1] e l'elettronica di controllo che deve gestire 3 assi in più.